Segmentation of blood vessels from medical images, such as magnetic resonance angiography (MRA) and computed tomography (CT) is a challenging problem with several applications important in diagnosis and surgery. Detection of stenosis and aneurysm and measuring tortuosity are examples where an accurate segmentation of the vasculature can help in the diagnosis. In practice these medical blood vessel images are often noisy and vessels might be broken. Our aim is a careful fairing of these structures and the closing of small gaps. Mathematically, we consider a geometric, variational approach. An energy encodes the fitting of the current vessel shape with a local classification, treated as a statistical local prior. As a suitable prior for vessels we consider long elongated ellipsoidal shapes oriented in the direction of the vessel. Thus, the energy is based on a strongly anisotropic area functional with a weighting term corresponding to these locally classified ellipsoidal master shapes.

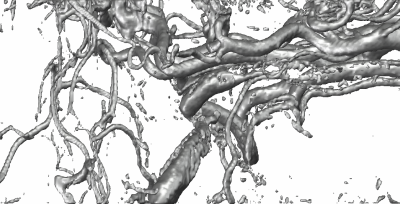
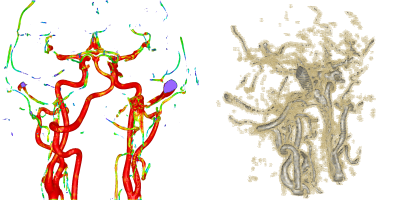This approach results in a significant, even though conservative, smoothing along the vessels. Noisy tubular like structures will develop a circular cross section and small gaps are closed. To identify the local prior we interpret the characteristic function of the blood vessels as a mass distribution and use moment analysis, that provide information about the shape and orientation of this distribution.

A careful local analysis is crucial for the robustness of the approach. Otherwise, tubular structures won't be recognized or nearby but separate vessels would have an influence on the local characterization. Furthermore, narrow band techniques are applied which reduce the computational load to a small neighborhood of the vessel structures (cf. the figure above).

Cooperation with: T. Tasdizen and R. Whitaker (University of Utah), C. Schaller (Neurosurgery Hospital at Bonn University)

<-- Uni/Mathematik