"BLaC-Wavelets und nicht ineinander geschachtelte Wavelets"

Nur hier, zum kostenlosen Download, ca. 1.9 MB, im PDF-Format, meine Diplomarbeit (tätä):

Diplomarbeit.pdf
Diplomarbeit.zip (ca. 1.7 MB)

Kurze Zusammenfassung:

Eine Multiskalenanalyse erlaubt die Repräsentation einer Funktion, bzw. gegebenen Daten, in verschiedenen Detailstufen (Leveln). Klassischerweise basieren diese unterschiedlichen Level auf einer Folge ineinander geschachtelter Funktionenräume. Mit zunehmendem Level konvergieren Approximationen in diesen Funktionenräumen gegen die Ausgangsdaten.
Im Fall der Haar-Wavelets sind dies z.B. Treppenfunkionen mit verschieden breiten Trägern. Je höher der Level ist, desto feiner werden die "Stufen", und desto genauer wird die Approximation.
G.P. Bonneau entwirft nun in seinem Artikel BLaC-wavelets and non-nested wavelets den theoretischen Hintergrund für eine Multiskalenanalyse mit nicht ineinander geschachtelten Räumen. Er beschreibt zwei Anwendungen:

BLaC-Wavelets sind eine von einem Parameter Delta abhängige Familie von Wavelets, mit denen es möglich ist eine stetige Vermischung des Haar-Wavelets und des linearen Wavelets zu definieren (BLaC = Blending of Linear and Constant). Die Skalierungsfunktion der Haar-Wavelets (Delta=0) bietet als Treppenfunktion eine perfekte Lokalität, ist aber nur sehr schlecht geeignet, stetige Daten zu approximieren. Eine bessere Regularität hierfür bietet die Hütchenfunktion, die Skalierungsfunktion des linearen Wavelets (Delta=1). Diese wiederum besitzt eine nicht so gute Lokalität und ist zum Darstellen unstetiger Daten weniger geeignet. Mit den BLaC-Wavelets ist es dem Anwender nun möglich, einen für ihn optimalen Kompromiss zwischen der perfekten Lokalität der Haar-Wavelets und der besseren Regularität der linearen Wavelets zu wählen.



Als zweite Anwendung der Multiskalenanalyse mit nicht ineinander geschachtelten Räumen sind hierarchische Triangulierungen aufgeführt. Hierbei wird eine gegebene Triangulierung in mehreren Schritten vereinfacht, d.h. die Anzahl der verwendeten Dreiecke wird reduziert. Hierfür existieren bereits eine Reihe Wavelet-basierter Verfahren, diese sind jedoch aufgrund der ineinander geschachtelten Räume immer mit Subdivision verbunden. Bonneau's Entwicklung erlaubt, sich nun davon zu lösen. Dies wird im letzten Teil der Arbeit geschildert.

Im ersten grösseren Teil der Arbeit wird das Konzept dieser neuen Multiskalenanalyse theoretisch eingeführt und erläutert. Anschliessend werden die BLaC-Wavelets definiert, wobei Bonneau's Ausführungen, z.B. durch eine Fehleranalyse, erheblich ergänzt werden. Verschiedene Eigenschaften der Skalierungsfunktionen werden aufgestellt und bewiesen. Anschliessend wird ein hauptsächlich der Anschauung dienender Implementierungsansatz ausführlich beschrieben und verwirklicht.

Die Theorie wird daraufhin noch auf zwei Dimensionen erweitert. Als Anwendung wird hier ein einfaches Bildkompressionsverfahren vorgestellt und implementiert. In Zusammenhang damit wird auch eine Methode zur Wahl des Parameters für ein gegebenes Bild entwickelt. Dies ist für ein ganzes Bild natürlich mit Vorsicht zu geniessen, da ein solcher Parameter meist nur lokal gut geeignet ist. Beim JPEG2000-Algorithmus existiert jedoch ein sogenanntes Region-of-Interest-Coding (s. www.jpg.org), in dem verschiedene Bildteile verschieden stark komprimiert werden. Für solche Bildteile wäre eine solcher Parameterwahl sicherlich sinnvoll.
Folgende Beispielbilder sollen verdeutlichen, dass ein Parameter Delta ungleich 0 oder 1 bessere Ergebnisse liefern kann als die reinen Haar- oder linearen Wavelets.

Originalbild Delta=0
Delta=0.5 Delta=1


Alle drei Bilder wurden auf ca. 60% Nullkoeffizienten reduziert. Es ist deutlich zu erkennen, dass die Haarwavelets (Delta=0) die Schärfe des Bildes erhalten, dafür aber deutliche und störende Blockeffekte auftreten. Diese sind bei den linearen Wavelets (Delta=1) vollständig verschwunden, das Bild ist jedoch verschwommen und unscharf.
Ein Kompromiss mit Delta=0.5 liefert hier ein besseres Ergebnis: Die Schärfe bleibt weitesgehend erhalten und die Blockeffekte sind fast nicht mehr vorhanden.


Aber dessen nicht genug! Zu dieser ca. 96 Seiten langen schriftlichen Ausführung gibt es noch drei ausführbare Programme, die das Dargelegte verdeutlichen sollen.

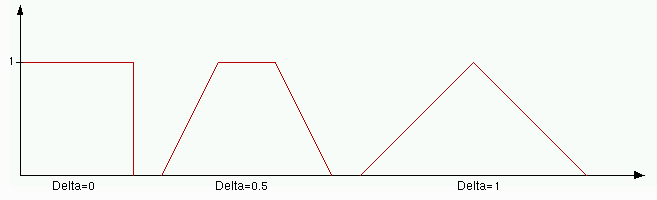
Das Programm MultiResol stellt eine Multiskalenanalyse grafisch dar. Hierbei kann der Parameter verändert und die Veränderungen in Echtzeit bewundert werden.
MRA2D stellt ebenfalls eine Multiskalenanalyse grafisch dar, jedoch für zweidimensionale Skalierungsfunktionen und Wavelets. Hierfür wird OpenGL benötigt.
ImgMRA präsentiert nun die Anwendung der BLaC-Wavelets: Ein Bildkompressionsalgorithmus. Passende SW-Bilder können eingeladen und mit verschiedenen Parametern verschieden stark komprimiert werden. Desweiteren lässt sich zu einem Bild ein mehr oder weniger optimaler Parameter Delta vorschlagen.


Und auch diese Programme kann man hier kostenlos downloaden:

MultiResol.exe
MRA2D.exe
ImgMRA.exe

Alle Programme sind unter Windows lauffähig, ich schätze ab Windows 95 ? Keine Ahnung, unter Windows 98 funktionieren sie jedenfalls. Anleitungen und Erklärungen finden sich in der Diplomarbeit.
Hinweis: Das Programm MRA2D benötigt OpenGL. Ist dieses nicht unter Windows installiert, müssen noch die DLL-Dateien cc3260mt.dll, rtl60.bpl und vcl60.bpl nach C: \Windows\ System kopiert werden.
Das Programm ImgMRA kann nur Schwarz-Weiss-Bilder im BMP-Format der Grösse (2^N)+1 x (2^N)+1 lesen. Da man solche Bilder ja nicht unbedingt immer parat hat, bzw. keine Lust hat seine Bilder in dieses gängige Format zu konvertieren, kann man sich hier die vier Beispielbilder meiner Diplomarbeit KOSTENLOS!!! herunterladen, um das Programm damit auszuprobieren.



zurück